«««Назад | Оглавление | Каталог библиотеки | Далее»»»

Прочитано: 26%

3. Алгоритмы

3.1 Предварительный фрактальный тест

         Как правило, структура естественных ландшафтов само-подобна в большом диапазоне размеров. Например, лунные кратеры с поперечниками от 10Е1 м до 10Е4 м имеют почти одинаковую форму. В отличие от само-подобных естественных ландшафтов, структура искусственных объектов выражена в более узком диапазоне размеров. Следовательно, возможные артифакты на изображении должны проявляться как аномалии в распределении пространственных деталей по размерам. В поиске таких аномалий и заключается смысл фрактального метода М.Стейна и М.Карлотто (лит.12, 13). К сожалению, их метод требует слишком много вычислений для обработки всех подходящих HIRES-изображений (около 80.000).
         Поэтому для той же цели использовался альтернативный, более простой алгоритм. Пусть M(r) есть распределение вероятности расстояний между локальными минимумами яркости вдоль горизонтальной строки изображения. Таким образом M(r) описывает распределение деталей изображения по размерам. На больших шкалах эту функцию можно аппроксимировать степенной функцией, характерной для фракталов:

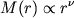
(1)

         Поскольку искусственные объекты имеют некий характерный размер, их присутствие должно увеличить среднеквадратичное отклонение M(r) от степенного закона, выражаемого линейной регрессией:

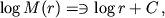
(2)

         где C является константой. Согласно эмпирическим результатам, M(r) у HIRES-изображений может быть аппроксимировано степенной функцией при r > 4 пикселов. Регрессия вычисляется при 4 < r < 31 пиксел (т.е. в диапазоне размеров от 50 до 900 м).
         Изображение разбивается на K=12 квадратов по 96x96 пикселов каждый. В каждой такой области методом наименьших квадратов вычисляется наилучшие параметры степенной функции, и находится среднеквадратичное отклонение от нее:

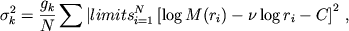
(3)

         где k - номер квадрата изображения; gk - множитель, компенсирующий вариации чувствительности сенсора в различных частях изображения; N - число размеров (шкал). Средняя дисперсия оценивается по этим региональным среднеквадратичным отклонениям.
         Анализ 733 HIRES-изображений, полученных через светофильтр на 0.75 микрона с орбит 112-115 (от полюсов вплоть до широт 75 градусов), показал что региональные среднеквадратичные отклонения распределяются по закону Гаусса. Согласно критерию Стьюдента для K=12 оценок, если в каком-либо квадрате выполняется неравенство

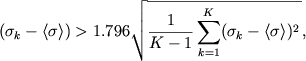
(4)

         эту область можно считать статистически аномальной с вероятностью 0,95.

«««Назад | Оглавление | Каталог библиотеки | Далее»»»