«««Назад | Оглавление | Каталог библиотеки | Далее»»»

Прочитано: 19%

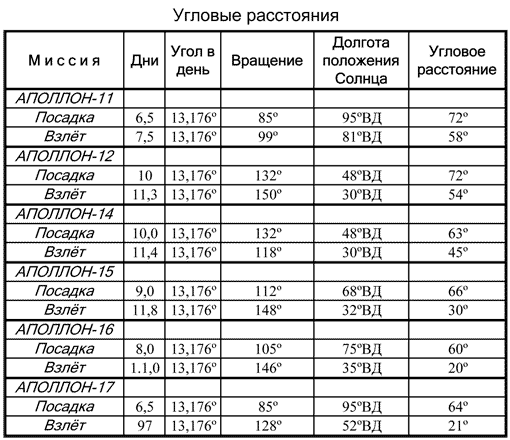
         Сначала вычислим положение Солнца в момент прилунения Аполлона-11. В столбце "Прилунение" таблицы данных по миссиям мы находим, что посадка на Луне произошла через 6,5 дней после новолуния. Умножив 6,5 дней на скорость вращения 13,176 град. в день, получаем 85 град. Вычитаем 85 град. из 180 град. и получаем долготу положения Солнца - 95 град. ВД. Аналогичным образом я вычислил долготу положения Солнца для всех лунных посадок и взлетов, что отражено в таблице угловых расстояний.
         Теперь необходимо найти угловое расстояние между точками положения Солнца и посадки на Луне. Оно равно: 95 град. (положение Солнца) - 23 град. (место посадки) = 72 град. Тот же процесс вычислений я использовал и для взлета: 81 град. (положение Солнца) - 23 град. = 58 град.
         Ниже приведена таблица угловых расстояний для посадок и взлетов всех экспедиций Аполлонов. Необходимо пояснить, что если обе точки находятся в одной долготе, то значения вычитаются - на рис. 16 слева показана схема посадки Аполлона-11. Если же точки имеют противоположную долготу, то значения складываются - справа на рис. 16 изображена схема взлета Аполлона-12.

Рис. 16. Слева: пункт А Восток - пункт В Восток, справа: пункт А Запад - пункт В Восток

Рис. 17. Слева: прилунение Аполлона-11, справа: сферический треугольник

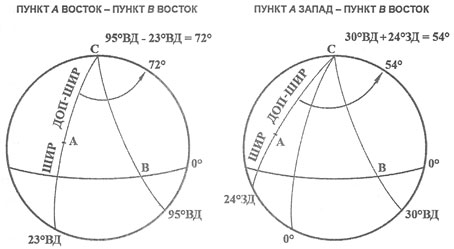
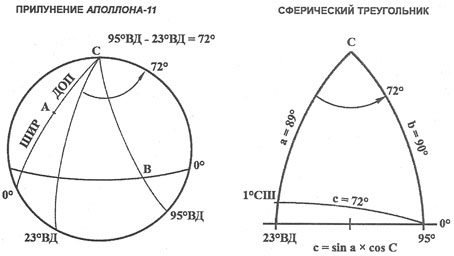
         Соединив эти точки с полюсом (точка С) и с экватором, получаем обычный навигационный треугольник. Две его стороны а и b - это ДОП-ШИР(A) и ДОП-ШИР(B) соответственно, С - угол между двумя сторонами, а третья сторона с - расстояние между двумя точками. Теперь это сферический треугольник. Уравнение для решения сферических треугольников, когда известны две стороны и угол между ними, выглядит следующим образом:
         cos с = cos a х cos b + (sin a x sin b x cos C).
         Поскольку b всегда равно 90 град., a cos 90 град. = 0, то первую часть уравнения можно опустить. У нас осталось: cos с = sin a х sin b х х cos С. Но поскольку sin 90 град. = 1, можно опустить и sin b. Окончательная формула уравнения выглядит так:
         cos с = sin a х cos С.
         На рис. 17 справа я использовал схему, более наглядно демонстрирующую сферический треугольник применительно к нашему случаю.
         с = acos (sin 89 град. x cos 72 град.).
         Значение с получается равным чуть больше 72 град. Угол возвышения Солнца в этот момент равен 90 град. - 72 град. = 18 град. Все остальные вычисления по посадкам и взлетам абсолютно аналогичны. Для момента взлета Аполлона-11 вычисляем:
         с = acos (sin 89 град. х cos 58 град.).
         Получаем значение чуть больше 58 град. Таким образом, угол возвышения Солнца в этот момент равен 90 град. - 58 град. = 32 град. То же самое проделываем и для остальных миссий.

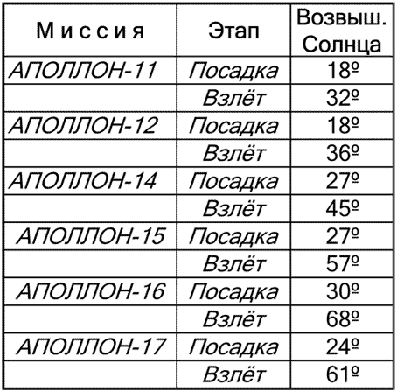
         На последней фотографии, где Олдрин и Армстронг чествуют флаг, тени произведены Солнцем, стоящим на высоте 34,9 град. над горизонтом. Максимальное возвышение Солнца в той экспедиции составляло 32 град., но разница в 2,9 град. явно недостаточна, чтобы делать какие-то выводы. Однако если учесть, что церемония поднятия флага является чуть ли не первым действием после каждой высадки и происходит в течение первых часов, то можно с уверенностью утверждать, что Солнце во время съемки находилось на высоте порядка 22 град. Проведенные вычисления вполне могут разбить утверждения NASA о реальности высадки астронавтов на Луне.

«««Назад | Оглавление | Каталог библиотеки | Далее»»»